sammenligning af afstanden ovenfor med CIE's system
Som nævnt er farveafstandene ovenfor målt på et tidspunkt hvor jeg ikke kendte
 CIE's afstandsformler for de 3 farveafstande
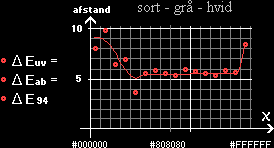
DEuv
DEab og
DE94 .
CIE's afstandsformler for de 3 farveafstande
DEuv
DEab og
DE94 .
Jeg har nu tegnet nogle grafer, hvor jeg har farverne liggende i afstanden 1p
ud af x-aksen, og ud af y-aksen afstanden mellem de to farver (som altid er 1p)
målt efter CIE's formler.
Hvis der var fuld overensstemmelse og ingen måleusikkerhed ville der blive 3
vandrette linier ud af det,
men der er stor måleusikkerhed i min udmåling af farver i afstanden 1p, og så
ville man forvente at målepunkterne lå tilfældigt spredt omkring de 3 vandrette
linier,
men det ses at spredningen ikke kun er tilfældig, så den skyldes ikke kun min
måleusikkerhed, men osse at ingen af formlerne for
DE-erne svarer særlig godt til øjets opfattelse
af afstanden mellem farverne.
| | | |
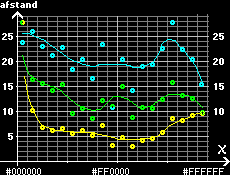
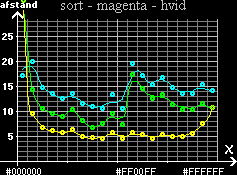
 Graf svarende til farvecirklen med 1p mellem farverne:
Graf svarende til farvecirklen med 1p mellem farverne:
 |
sort - rød - hvid
|
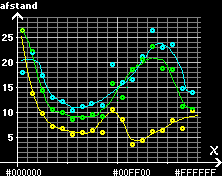
sort - grøn - hvid
|

|
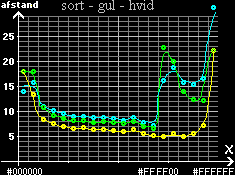
|
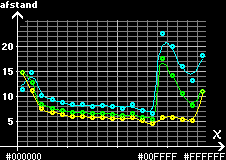
sort - cyan - hvid
|
|
|
| |
Statistisk, hvor mange CIE-enheder svarer til 1p: |
| |
DEuv : |
snit = 14,5 | ± 5,6 | (± 63 % ) |
| DEab : |
snit = 11,9 | ± 5,5 | (± 46 % ) |
| DE94 : |
snit = 7,0 | ± 4,4 | (± 39 % ) |
|
|